Learning
Before Paul de Casteljau developed an algorithm for it, before Pierre Bézier popularized it, and the Bézier curve became essential to computer graphics, Mary Everest Boole(1) was having her math students thread straight lines of yarn through holes in paper to see the curve appear.
She called it ‘curve stitching,’ now referred to as string art. Boole knew that humans learn with all their senses.
When we were a child someone pointed to the animal and said, “Dog!” We learned that if it had four legs, fur, and barked, no matter the size or color, it was a “dog.”
Someone also pointed to the curvy red line on the wooden block and said, “two.” We soon learned that the name ‘two’ was not the wooden block in the same way the word ‘dog’ was always the animal, because they also said, “One, two!” while raising different fingers in succession with each sound. They also placed ‘one, two’ cookies on a plate. And we understood ‘two’ to be not a thing, but something to do with having more. And fingers. Fingers became a way to show how many. And the curvy line. The curvy line became the way to draw one more than ‘one.’
Then came doubling and halving and the number two flowed with us into the world of a language that has the power to take humans to Mars. A language to predict the future and explain things from light-years in the past. A way to talk with each other about interactions and outcomes, with its own alphabet and terminology.
Math
The alphabets have differed over time: Mayan dots and bars, Mesopotamian cuneiform impressions, Chinese oracle bone scripts, beads on an abacus, knots on a string. But there have always been pictures. Even those fluent in the notation need pictures. Certainly, the rest of us who aren’t fluent do.

c) Rama, Cc-by-sa-2.0-fr
Louvre Museum / CC BY-SA 2.0 FR (creativecommons.org/licenses)
This is an image of a heptagon with calculations on a clay tablet from the first half of the second millennium BCE, found in the ancient city of Susa. Scholars think it may be a geometry problem from a school for scribes.
Drawing
Middle Stone Age people were carving geometric patterns in rocks 70,000 years BCE in caves in what is now South Africa.(2) Scholars debate when humans first used math, but I’m going to assume it was when they realize they had fingers and wanted more than one cookie. The Mayans used a system of base 20 (3)after all. I also assume humans started to draw the moment they dragged the tip of a stick through the dirt and could explain where the tree with the good fruit was in relation to the bend in the stream.
Why do we draw? I think we draw for the same reasons we use mathematics:
- to understand, organize
- to record, remember
- to communicate, share
- to create, enjoy
Proportion, the golden ratio, perspective, tessellation, symmetry … math and art are inseparably intertwined. Math helps us depict the world we can touch, and the abstract we can only imagine. Things too small, too large, too many, too far away, or possibilities we are not yet sure exist.
So we use graphs, and Venn, Hasse, Euler, and Voronoi diagrams to provide clarity, reveal the patterns, sizes, and relationships. This:
![]()
with this:
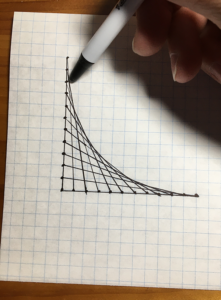
Are back-of-the-envelope and paper napkin drawings still a thing among engineers in the digital age? I hope so, and I hope they save them all.
Those of us who are not using the equations for useful work can simply enjoy the beauty in the art, the elegance of the concepts, derive hope from the potential, and celebrate the human capacity for imagining. Someday there will be cave drawings on Mars.
1. Yes, that Everest. Yes, that Boole. In the 1800s: VALENTE, K. (2010). Giving wings to logic: Mary Everest Boole’s propagation and fulfilment of a legacy. The British Journal for the History of Science, 43(1), 49-74. doi:10.1017/S0007087409990380
2. Article (with images) about the Blombos cave rocks: https://phys.org/news/2018-09-piece-silcrete-blombos-cave-predates.html
3. Mayan math: https://mayaarchaeologist.co.uk/2016/12/28/maya-numbers/
